What Is the Greatest Integer Function?
Practice Problems

Examining the number line near 12 we see that $$\lfloor 12.5\rfloor = 12$$ .

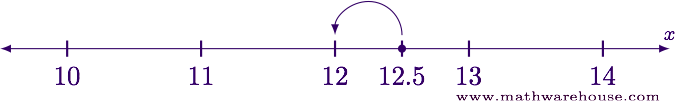
Examining the number line near -6.7 we see that $$\lfloor -6.7\rfloor = -7$$ .

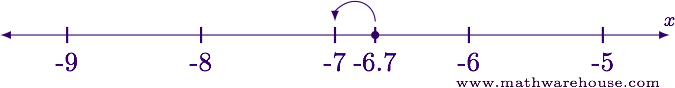
Since 50 is an integer, we know $$\lfloor 50\rfloor = 50$$ .

Problem 2

Evaluate the following.

1. $$\lfloor \pi \rfloor$$
2. $$\left\lfloor \frac\right\rfloor$$
3. $$\lfloor \sqrt 2\rfloor$$

Using a calculator, we can determine that $$\pi$$ is approximately 3.14. Examining the number line near this point we see that $$\lfloor \pi\rfloor = 3$$ .

Using a calculator, we can determine that $$\frac$$ is approximately 1.21. Examining the number line near this point we see that $$\left\lfloor \frac\right\rfloor = 1$$ .

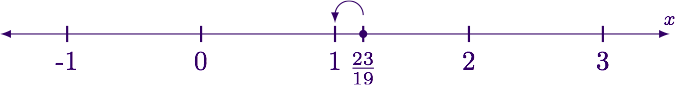
Using a calculator, we can determine that $$\sqrt 2$$ is approximately 1.41. Examining the number line near this point we see that $$\left\lfloor \sqrt 2\right\rfloor = 1$$ .

Problem 3

Sketch a graph of $$y = \lfloor 2x \rfloor$$ .

As in the previous example, we can go about this by constructing a table, or interpreting the function in terms of transformations. This solution will do both.

$$ \begin <|c|c|c|>\hline x & 2x & \lfloor 2x \rfloor \\ \hline -0.75 & -1.5 & -2\\ -0.5 & -1 & -1\\ -0.25 & -0.5 & -1\\ 0 & 0 & 0\\ 0.25 & 0.5 & 0\\ 0.5 & 1 & 1\\ 0.75 & 1.5 & 1\\ 1 & 2 & 2\\ 1.25 & 2.5 & 2\\ \hline \end $$

In this case, we see that every time $$x$$ is a multiple of 0.5 the function jumps to the next higher integer.

We can interpret $$y = \lfloor 2x \rfloor$$ as a horizontal compression by a factor of 2. That is, each of the $$x$$-values from $$y = \lfloor x\rfloor$$ gets cut in half, but the $$y$$-values stay the same.

Problem 4

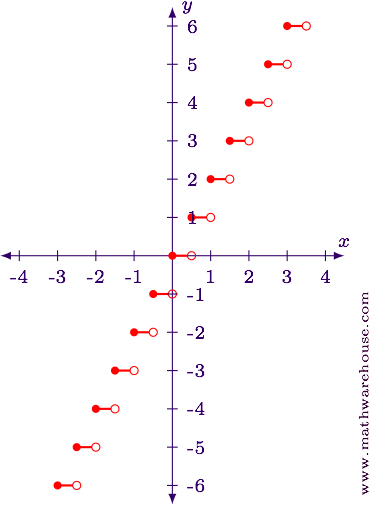
Sketch a graph of $$y = \lfloor 1.5x \rfloor$$ .

We will examine this function using both a table, and then as a transformation of functions.

$$ \begin <|c|c|c|>\hline x & 1.5x & \lfloor 1.5x \rfloor \\ \hline -1 & -1.5 & -2\\ -2/3 & -1 & -1\\ -1/3 & -0.5 & -1\\ 0 & 0 & 0\\ 1/3 & 0.5 & 0\\ 2/3 & 1 & 1\\ 1 & 1.5 & 1\\ 4/3 & 2 & 2\\ 5/3 & 2.5 & 2\\ 2 & 3 & 3\\ \hline \end $$

The table shows that the function increases every multiple of 2/3.

Since the variable $$x$$ is being multiplied by 1.5, we know that the graph of $$y = \lfloor x\rfloor$$ is being compressed horizontally.

Problem 5

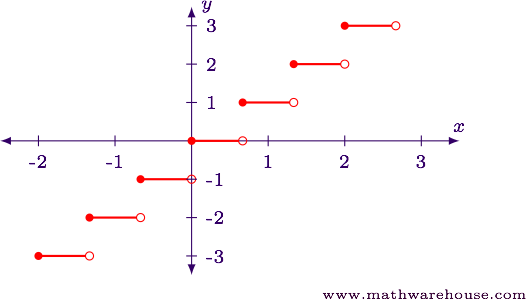
Sketch a graph of $$y = \lfloor -0.25x\rfloor$$ .

We will examine this function using both a table, and then as a transformation of functions.

$$ \begin <|c|c|c|>\hline x & -0.25x & \lfloor -0.25x \rfloor \\ \hline -4 & 1 & 1\\ -3 & 0.75 & 0\\ -2 & 0.5 & 0\\ -1 & 0.25 & 0\\ 0 & 0 & 0\\ 1 & -0.25 & -1\\ 2 & -0.5 & -1\\ 3 & -0.75 & -1\\ 4 & -1 & -1\\ \hline \end $$

The table shows that the function increases every multiple of 4.

Since the variable $$x$$ is being multiplied by 0.25, we know the function is being horizontally stretched by a factor of 4. Since the coefficient is negative, the function is also being reflected about the $$y$$-axis.

Problem 6

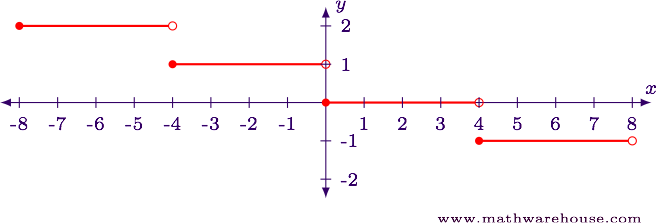
Sketch a graph of $$y = 2\lfloor x\rfloor$$ .

We will examine this function using both a table, and then as a transformation of functions.

$$ \begin <|c|c|c|>\hline x & \lfloor x \rfloor & 2\lfloor x \rfloor\\ \hline -1.5 & -2 & -4\\ -1 & -1 & -2\\ -0.5 & -1 & -2\\ 0 & 0 & 0\\ 0.5 & 0 & 0\\ 1 & 1 & 2\\ 1.5 & 1 & 2\\ 2 & 2 & 4\\ \hline \end $$

The table shows that the function increases by 2 every time $$x$$ increases by 1.

The function has a vertical stretch by 2.

Problem 7

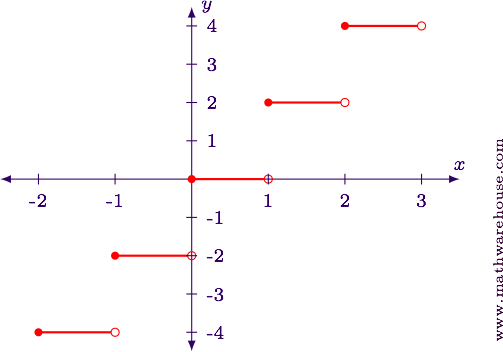
Sketch a graph of $$y = \lfloor x + 3\rfloor$$ .

We will examine this function using both a table, and then as a transformation of functions.

$$ \begin <|c|c|c|>\hline x & x + 3 & \lfloor x + 3\rfloor \\ \hline -4 & -1 & -1\\ -3.5 & -0.5 & -1\\ -3 & 0 & 0\\ -2.5 & -0.5 & 0\\ -2 & 1 & 1\\ -1.5 & 1.5 & 1\\ -1 & 2 & 2\\ -0.5 & 2.5 & 2\\ 0 & 3 & 3\\ 0.5 & 3.5 & 3\\ 1 & 4 & 4\\ \hline \end $$

The table shows us that the function increases each time $$x$$ is an integer.

The function $$y = \lfloor x + 3\rfloor$$ is a shift to the left by 3 units of the function $$y = \lfloor x \rfloor$$ .

Problem 8

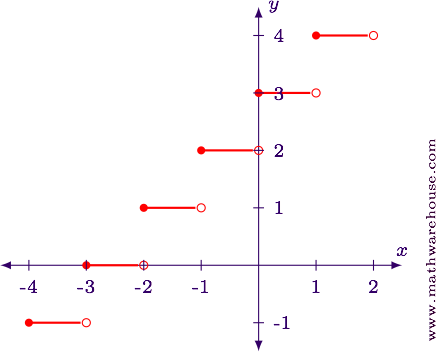
Sketch a graph of $$y = -0.75\lfloor 2 - x\rfloor$$ .

We will examine this function using both a table, and then as a transformation of functions.

$$ \begin <|c|c|c|c|>\hline x & 2 - x & \lfloor 2 - x \rfloor & -0.75\lfloor 2 - x \rfloor\\ \hline -2.5 & 4.5 & 4 & 3\\ -2 & 4 & 4 & 3\\ -1.5 & 3.5 & 3 & 2.25\\ -1 & 3 & 3 & 2.25\\ -0.5 & 2.5 & 2 & 1.5\\ 0 & 2 & 2 & 1.5\\ 0.5 & 1.5 & 1 & 0.75\\ 1 & 1 & 1 & 0.75\\ 1.5 & 0.5 & 0 & 0\\ 2 & 0 & 0 & 0\\ 2.5 & -0.5 & -1 & -0.75\\ \hline \end $$

The table shows that the function changes value just after $$x$$ is an integer. Each time the function changes value it decreases by 0.75.

The function $$y = -0.75\lfloor 2 - x\rfloor$$ consists of four different transformations.

1. A vertical reflection (over the $$x$$-axis).
2. A horizontal reflection (over the $$y$$-axis).
3. A vertical compression of 0.75.
4. A horizontal shift by 2 units to the right.